Here below a little program in C++/CLI that implements 2 classes (in fact, they are 3). There is the main class, called Fiborial (Fibo(nnacci)+(Facto)rial) that implements the Fibonacci and the Factorial algorithms in two ways, one Recursive (using recursion) and the other Imperative (using loops and states). The second class is just an instance class that does the same thing, but its there just to show the difference between static and instance classes, and finally the third one (which will not appear in other languages) is the Program class which has the static execution method "Main".
You can also find 3 more little examples at the bottom. One prints out the Factorial's Series and Fibonacci's Series, the second one just shows a class that mixes both: static and instance members, and finally the third one that uses different return types (including System::Numerics::BigInteger) for the Factorial method to compare the timing and result.
As with the previous posts, you can copy and paste the code below in your favorite IDE/Editor and start playing and learning with it. This little "working" program will teach you some more basics of the Programming Language.
There are some "comments" on the code added just to tell you what are or how are some features called. In case you want to review the theory, you can read my previous post, where I give a definition of each of the concepts mentioned on the code. You can find it here: http://carlosqt.blogspot.com/2011/01/new-series-factorial-and-fibonacci.html
The Fiborial Program
// Factorial and Fibonacci in C++/CLI
#include "stdafx.h"
using namespace System;
using namespace System::Collections::Generic;
using namespace System::Diagnostics;
using namespace System::Numerics;
namespace FiborialCpp {
// static class
static ref class StaticFiborial {
private:
// Static Field
static String^ className;
// Static Constructor
static StaticFiborial() {
className = L"Static Constructor";
Console::WriteLine(className);
}
public:
// Static Method - Factorial Recursive
static BigInteger FactorialR(int n) {
if (n == 1)
return 1;
else
return n * FactorialR(n - 1);
}
// Static Method - Factorial Imperative
static BigInteger FactorialI(int n) {
BigInteger res = 1;
for (int i = n; i >= 1; i--) {
res *= i;
}
return res;
}
// Static Method - Fibonacci Recursive
static long FibonacciR(int n) {
if (n < 2)
return 1;
else
return FibonacciR(n - 1) + FibonacciR(n - 2);
}
// Static Method - Fibonacci Imperative
static long FibonacciI(int n) {
long pre, cur, tmp = 0;
pre = cur = 1;
for (int i = 2; i <= n; i++) {
tmp = cur + pre;
pre = cur;
cur = tmp;
}
return cur;
}
// Static Method - Benchmarking Algorithms
static void BenchmarkAlgorithm(int algorithm, List<int>^ values) {
Stopwatch ^timer = gcnew Stopwatch();
int i, testValue;
BigInteger facTimeResult = 0;
long fibTimeResult = 0;
i = testValue = 0;
// "Switch" Flow Constrol Statement
switch (algorithm)
{
case 1:
Console::WriteLine("\nFactorial Imperative:");
// "For" Loop Statement
for (i = 0; i < values->Count; i++)
{
testValue = values[i];
// Taking Time
timer->Start();
facTimeResult = FactorialI(testValue);
timer->Stop();
// Getting Time
Console::WriteLine(" ({0}) = {1}", testValue, timer->Elapsed);
}
break;
case 2:
Console::WriteLine("\nFactorial Recursive:");
// "While" Loop Statement
while (i < values->Count)
{
testValue = values[i];
// Taking Time
timer->Start();
facTimeResult = FactorialR(testValue);
timer->Stop();
// Getting Time
Console::WriteLine(" ({0}) = {1}", testValue, timer->Elapsed);
i++;
}
break;
case 3:
Console::WriteLine("\nFibonacci Imperative:");
// "Do-While" Loop Statement
do {
testValue = values[i];
// Taking Time
timer->Start();
fibTimeResult = FibonacciI(testValue);
timer->Stop();
// Getting Time
Console::WriteLine(" ({0}) = {1}", testValue, timer->Elapsed);
i++;
} while (i < values->Count);
break;
case 4:
Console::WriteLine("\nFibonacci Recursive:");
// "For Each" Loop Statement
for each (int item in values)
{
testValue = item;
// Taking Time
timer->Start();
fibTimeResult = FibonacciR(testValue);
timer->Stop();
// Getting Time
Console::WriteLine(" ({0}) = {1}", testValue, timer->Elapsed);
}
break;
default:
Console::WriteLine(L"DONG!");
break;
}
}
};
// Instance Class
public ref class InstanceFiborial {
// Instance Field
String^ className;
// Instance Constructor
public:
InstanceFiborial() {
this->className = "Instance Constructor";
Console::WriteLine(this->className);
}
// Instance Method - Factorial Recursive
BigInteger FactorialR(int n) {
// Calling Static Method
return StaticFiborial::FactorialR(n);
}
// Instance Method - Factorial Imperative
BigInteger FactorialI(int n) {
// Calling Static Method
return StaticFiborial::FactorialI(n);
}
// Instance Method - Fibonacci Recursive
long FibonacciR(int n) {
// Calling Static Method
return StaticFiborial::FibonacciR(n);
}
// Instance Method - Factorial Imperative
long FibonacciI(int n) {
// Calling Static Method
return StaticFiborial::FibonacciI(n);
}
};
};
int main(array<System::String ^> ^args)
{
Console::WriteLine("\nStatic Class");
// Calling Static Class and Methods
// No instantiation needed. Calling method directly from the class
Console::WriteLine("FacImp(5) = {0}", FiborialCpp::StaticFiborial::FactorialI(5));
Console::WriteLine("FacRec(5) = {0}", FiborialCpp::StaticFiborial::FactorialR(5));
Console::WriteLine("FibImp(11)= {0}", FiborialCpp::StaticFiborial::FibonacciI(11));
Console::WriteLine("FibRec(11)= {0}", FiborialCpp::StaticFiborial::FibonacciR(11));
Console::WriteLine("\nInstance Class");
// Calling Instance Class and Methods
// Need to instantiate before using. Calling method from instantiated object
FiborialCpp::InstanceFiborial ^ff = gcnew FiborialCpp::InstanceFiborial();
Console::WriteLine("FacImp(5) = {0}", ff->FactorialI(5));
Console::WriteLine("FacRec(5) = {0}", ff->FactorialR(5));
Console::WriteLine("FibImp(11)= {0}", ff->FibonacciI(11));
Console::WriteLine("FibRec(11)= {0}", ff->FibonacciR(11));
// Create a (generic) list of integer values to test
// From 5 to 50 by 5
List<int> ^values = gcnew List<int>();
for(int i = 5; i <= 50; i += 5)
values->Add(i);
// Benchmarking Fibonacci
// 1 = Factorial Imperative
FiborialCpp::StaticFiborial::BenchmarkAlgorithm(1, values);
// 2 = Factorial Recursive
FiborialCpp::StaticFiborial::BenchmarkAlgorithm(2, values);
// Benchmarking Factorial
// 3 = Fibonacci Imperative
FiborialCpp::StaticFiborial::BenchmarkAlgorithm(3, values);
// 4 = Fibonacci Recursive
FiborialCpp::StaticFiborial::BenchmarkAlgorithm(4, values);
// Stop and Exit
Console::Read();
return 0;
}
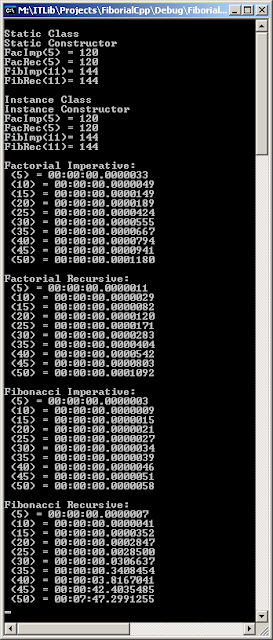
And the Output is:
Humm, looks like Fibonnaci's algorithm implemented using recursion is definitively more complex than the others 3 right? I will grab these results for this and each of the upcoming posts to prepare a comparison of time execution between all the programming languages, then we will be able to talk about the algorithm's complexity as well.
Printing the Factorial and Fibonacci Series
#include "stdafx.h"
using namespace System;
using namespace System::Text;
using namespace System::Numerics;
namespace FiborialSeries {
static ref class Fiborial {
public:
// Using a StringBuilder as a list of string elements
static String^ GetFactorialSeries(int n) {
// Create the String that will hold the list
StringBuilder ^series = gcnew StringBuilder();
// We begin by concatenating the number you want to calculate
// in the following format: "!# ="
series->Append("!");
series->Append(n);
series->Append(" = ");
// We iterate backwards through the elements of the series
for (int i = n; i <= n && i > 0; i--) {
// and append it to the list
series->Append(i);
if (i > 1)
series->Append(" * ");
else
series->Append(" = ");
}
// Get the result from the Factorial Method
// and append it to the end of the list
series->Append(Factorial(n));
// return the list as a string
return series->ToString();
}
// Using a StringBuilder as a list of string elements
static String^ GetFibonnaciSeries(int n)
{
// Create the String that will hold the list
StringBuilder ^series = gcnew StringBuilder();
// We begin by concatenating the first 3 values which
// are always constant
series->Append("0, 1, 1");
// Then we calculate the Fibonacci of each element
// and add append it to the list
for (int i = 2; i <= n; i++)
{
if (i < n)
series->Append(", ");
else
series->Append(" = ");
series->Append(Fibonacci(i));
}
// return the list as a string
return series->ToString();
}
static BigInteger Factorial(int n)
{
if (n == 1)
return 1;
else
return n * Factorial(n - 1);
}
static long Fibonacci(int n)
{
if (n < 2)
return 1;
else
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
};
};
using namespace FiborialSeries;
int main(array<System::String ^> ^args)
{
// Printing Factorial Series
Console::WriteLine();
Console::WriteLine(Fiborial::GetFactorialSeries(5));
Console::WriteLine(Fiborial::GetFactorialSeries(7));
Console::WriteLine(Fiborial::GetFactorialSeries(9));
Console::WriteLine(Fiborial::GetFactorialSeries(11));
Console::WriteLine(Fiborial::GetFactorialSeries(40));
// Printing Fibonacci Series
Console::WriteLine();
Console::WriteLine(Fiborial::GetFibonnaciSeries(5));
Console::WriteLine(Fiborial::GetFibonnaciSeries(7));
Console::WriteLine(Fiborial::GetFibonnaciSeries(9));
Console::WriteLine(Fiborial::GetFibonnaciSeries(11));
Console::WriteLine(Fiborial::GetFibonnaciSeries(40));
Console::Read();
return 0;
}
And the Output is:
Mixing Instance and Static Members in the same Class
We can also define instance classes that have both, instance and static members such as: fields, properties, constructors, methods, etc. However, we cannot do that if the class is marked as static because of the features mentioned in the previous post:
The main features of a static class are:
- They only contain static members.
- They cannot be instantiated.
- They are sealed.
- They cannot contain Instance Constructors
#include "stdafx.h"
using namespace System;
namespace FiborialExtrasCpp2 {
// Instance Classes can have both: static and instance members.
// However, Static Classes only allow static members to be defined.
// If you declare our next example class as static
// (static class Fiborial) you will get the following compile error
// Error: cannot declare instance members in a static class
// Instance Class
ref class Fiborial {
// Instance Field
private:
int instanceCount;
// Static Field
static int staticCount;
public:
// Instance Read-Only Property
// Within instance members, you can always use
// the "this" reference pointer to access your (instance) members. s
property int InstanceCount {
int get() { return this->instanceCount; }
}
// Static Read-Only Property
// Remeber that Properties are Methods to the CLR, so, you can also
// define static properties for static fields.
// As with Static Methods, you cannot reference your class members
// with the "this" reference pointer since static members are not
// instantiated.
static property int StaticCount {
int get() { return staticCount; }
}
// Instance Constructor
Fiborial() {
this->instanceCount = 0;
Console::WriteLine("\nInstance Constructor {0}", this->instanceCount);
}
// Static Constructor
static Fiborial() {
staticCount = 0;
Console::WriteLine("\nStatic Constructor {0}", staticCount);
}
// Instance Method
void Factorial(int n) {
this->instanceCount += 1;
Console::WriteLine("\nFactorial({0})", n);
}
// Static Method
static void Fibonacci(int n) {
staticCount += 1;
Console::WriteLine("\nFibonacci({0})", n);
}
};
};
using namespace FiborialExtrasCpp2;
int main(array<System::String ^> ^args)
{
// Calling Static Constructor and Methods
// No need to instantiate
Fiborial::Fibonacci(5);
// Calling Instance Constructor and Methods
// Instance required
Fiborial ^fib = gcnew Fiborial();
fib->Factorial(5);
Fiborial::Fibonacci(15);
fib->Factorial(5);
// Calling Instance Constructor and Methods
// for a second object
Fiborial ^fib2 = gcnew Fiborial();
fib2->Factorial(5);
Console::WriteLine();
// Calling Static Property
Console::WriteLine("Static Count = {0}", Fiborial::StaticCount);
// Calling Instance Property of object 1 and 2
Console::WriteLine("Instance 1 Count = {0}", fib->InstanceCount);
Console::WriteLine("Instance 2 Count = {0}", fib2->InstanceCount);
Console::Read();
return 0;
}
And the Output is:
Factorial using System::Int64, System::Double, System::Numerics::BigInteger
The Factorial of numbers over 20 are massive!
For instance: !40 = 815915283247897734345611269596115894272000000000!
Because of this, the previous version of this program was giving the "wrong" result
!40 = -70609262346240000 when using "long" (System::Int64) type, but it was on my previous post in VB.NET that I realized about this faulty code, because instead of giving me a wrong value, VB.NET execution thrown an Overflow Exception when using the "Long" (System::Int64) type.
My first idea was to use ulong and ULong, but both failed for "big" numbers. I then used Double (double floating point) type and got no more exception/wrong result. The result of the factorial was now correct !40 = 1.1962222086548E+56, but still I wanted to show the Integer value of it, so I did some research and found that there is a new System::Numerics::BigInteger class in the .NET Framework 4.0. Adding the reference to the project and using this new class as the return type of the Factorial methods, I was able to get the result I was expecting.
!40 = 815915283247897734345611269596115894272000000000
What I also found was that using different types change the time the algorithm takes to finish:
System::Int64 < System::Double < System::Numerics::BigInteger
Almost by double!
To illustrate what I just "tried" to say, lets have a look at the following code and the output we get.
#include "stdafx.h"
using namespace System;
using namespace System::Numerics;
using namespace System::Diagnostics;
// Long Factorial
static Int64 FactorialInt64(int n) {
if (n == 1)
return 1;
else
return n * FactorialInt64(n - 1);
}
// Double Factorial
static Double FactorialDouble(int n) {
if (n == 1)
return 1;
else
return n * FactorialDouble(n - 1);
}
// BigInteger Factorial
static BigInteger FactorialBigInteger(int n) {
if (n == 1)
return 1;
else
return n * FactorialBigInteger(n - 1);
}
int main(array<System::String ^> ^args) {
Stopwatch ^timer = gcnew Stopwatch();
Int64 facIntResult = 0;
Double facDblResult = 0;
BigInteger facBigResult = 0;
Console::WriteLine("\nFactorial using Int64");
// Benchmark Factorial using Int64
for (int i = 5; i <= 50; i += 5)
{
timer->Start();
facIntResult = FactorialInt64(i);
timer->Stop();
Console::WriteLine(" ({0}) = {1} : {2}", i, timer->Elapsed, facIntResult);
}
Console::WriteLine("\nFactorial using Double");
// Benchmark Factorial using Double
for (int i = 5; i <= 50; i += 5)
{
timer->Start();
facDblResult = FactorialDouble(i);
timer->Stop();
Console::WriteLine(" ({0}) = {1} : {2}", i, timer->Elapsed, facDblResult);
}
Console::WriteLine("\nFactorial using BigInteger");
// Benchmark Factorial using BigInteger
for (int i = 5; i <= 50; i += 5)
{
timer->Start();
facBigResult = FactorialBigInteger(i);
timer->Stop();
Console::WriteLine(" ({0}) = {1} : {2}", i, timer->Elapsed, facBigResult);
}
Console::Read();
return 0;
}
NOTE: you need to manually add a reference to the System.Numerics.dll assembly to your project so you can add it to your code.
And the Output is:








No comments:
Post a Comment